这是我的第一篇博文(拖了很久才放上来)
主要内容是关于Clustering中最基本的一个k-means以及相关的几个变种
算是个人学习过程中一个笔记(以及一个的讲稿)，因此有些地方可能写的不是很清楚,下次改正！

Clustering: K-means

---

Clustering

将类似的东西分到一组，属于Unsupervised learning 不需要训练集进行训练。

example:将一群人分为几组，提取N种特征组成一个N维向量。

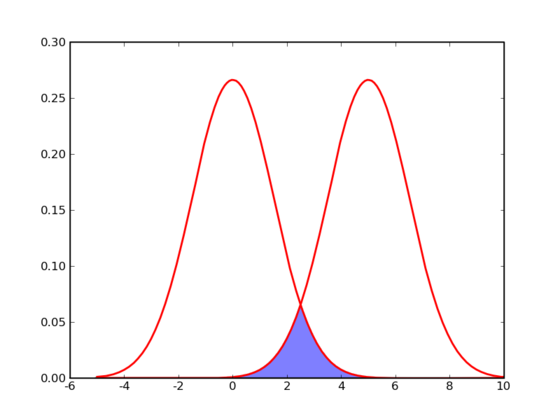
图中的阴影部分为可能会猜错的部分，错误是无可避免的

K-means

基于这个假设，如果要一共有n个数要分为K类，K-means所要优化的目标函数即为：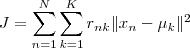

(n在ClusterK中时，Tnk = 1，else = 0）

直接采用迭代的方法：先固定一个数，寻找到最优的另一个数：先固定uk ，选择最优的Tnk,可见将数据点归类到离他最近的那个中心，再固定Tnk，求uk，J对uk求导
J最小时满足：

优点： easy to implement
缺点： 可能收敛到局部最小值，在大规模的数据集处理较慢

K-means不能保证是最优解！！！

K-means 具体过程

随机选取k个点作为质心
do
    将每个点归类到最近的质心
    形成k个簇
while 簇变化或达到最大次数

• Step
  1. 选择一个k值，即将数据分为多少类。可以判断k的好坏或者根据需求
  2. 随机选择最初的质心，可以用多次取均值，也可以使用bisecting K-means
  3. 将数据集中所有的店都计算下与质心的距离，分到离他最近的那类，然后将每个簇算出平均值，以这个点作为新的指点。反复重复这两步

kmeans的相关优化

• kmeans 的缺陷

  1. 分为几个k值是认为给定的，最优的k值的难以确定(canopy算法)

  2. 需要人为确定初始的聚类中心，不同的中心导致不同的聚类结果（举例说明)
     （可采用层级聚类，遗传算法来确定初始的聚类）

     这里采用k-means++来弥补第二种缺陷：
     即初始时定位的聚类中心要尽可能远：

• 核心步骤
  1. 随机选择一个点作为第一个聚类中心
  2. 对于剩余的每一个点，计算它与最近的中心距离
  3. 距离越大的点，被选为中心的概率越大
  4. 重复2.3,到 k 簇**

     D(x) = dist(x,nearst_central)
        random(0,sum(D(x)))
        i in range x
        {random -=D(i)}
        while random >= 0
        this i = new_central  
     

---

Extra

K-medoids

K-means 算法取平均值可以取到空间中的任意值，但对数据的要求比较高（举例说明）
适用对象：升高，图像RGB值等
当面对用户聚类或物品聚类的时候不适用！

K-medoids 选取中位数
优势： 不宜受到离群点的干扰

将欧式距离改为: